Indirect optellen. Een vergeten strategie voor het oplossen van aftrekopgaven?

Bij het gebruik van indirect optellen berekent men het verschil door vanaf de aftrekker verder te tellen of te rekenen tot het aftrektal is bereikt, bijvoorbeeld 343 – 187 oplossen via 187 + 13 = 200; 200 + 100 = 300; 300 + 43 = 343; en 13 + 100 + 43 = 156. Hoewel deze strategie in Vlaanderen geen onderdeel is van het standaard lespakket voor kinderen, tonen mijn resultaten dat indirect optellen erg efficiënt en adaptief wordt toegepast door veel Vlaamse negen- tot twaalfjarigen. Daarnaast blijkt dat de wiskundige conceptuele kennis die kinderen hebben van belang is voor het adaptief gebruik van de indirect optelstrategie.[1]

Strategieën voor het oplossen van meercijferige aftrekopgaven

Kinderen kunnen meercijferige aftrekopgaven, zoals 86 – 42 of 504 − 276, op verschillende manieren aanpakken. Naast het gebruik van een zakrekenmachine en cijferend rekenen, kunnen zij de opgave uit het hoofd uitrekenen. Kinderen kunnen bijvoorbeeld gebruikmaken van direct aftrekken, waarbij 504 − 276 wordt opgelost door stapsgewijs 200, 70 en 6 weg te nemen van 504 om het verschil van 228 te berekenen. Een andere hoofdrekenstrategie is indirect optellen, waarbij men het verschil berekent door vanaf de aftrekker verder te tellen of te rekenen tot het aftrektal is bereikt; dus 504 – 276 oplossen via 276 + 24 = 300; 300 + 200 = 500; 500 + 4 = 504; en 24 + 200 + 4 = 228.

Zowel in de Vlaamse eindtermen voor het lager onderwijs (Onderwijs Vlaanderen, 2023) als de Nederlandse kerndoelen (Stichting Leerplan Ontwikkeling, 2006) is het gebruik van verschillende rekenstrategieën een belangrijke onderwijsdoelstelling. Het is echter niet enkel van belang dat kinderen verschillende rekenstrategieën kennen en kunnen gebruiken; ook het selecteren van de meest adaptieve strategie is belangrijk. Hoewel er verschillende definities voor deze term bestaan, verwijst strategieadaptiviteit doorgaans naar het aanpassen van een strategiekeuze aan de numerieke karakteristieken van de gegeven rekenopgaven.  Zo kan je bijvoorbeeld 588 – 16 beter oplossen met direct aftrekken door middel van ‘588 – 10 = 578’ gevolgd door ‘578 – 6 = 572’ dan door middel van indirect optellen, eerst ‘16 + 84 = 100’ en dan ‘100 + 400 = 500; 500 + 88 = 588’ en ‘84 + 400 + 88 = 572’, omdat de eerstgenoemde strategie eenvoudiger is voor deze opgave, en de kans op fouten dus een stuk kleiner is. Voor het oplossen van meercijferige aftrekopgaven met een klein verschil tussen het aftrektal en de aftrekker, zoals bijvoorbeeld ‘614 − 586 = 28’, wordt indirect optellen vaak gezien als een bijzonder adaptieve strategie. Hoewel rationeel gezien indirect optellen inderdaad een efficiënte strategie lijkt voor het oplossen van aftrekopgaven met een klein verschil, krijgt deze strategie in het Vlaamse rekenonderwijs nauwelijks aandacht (Torbeyns et al., 2018). Ook in het wiskundeonderwijs in Nederland wordt aan indirect optellen niet veel aandacht besteed (Hickendorff, 2020).

Indirect optellen: Een vergeten strategie voor het oplossen van aftrekopgaven?

Voorgaand onderzoek naar het gebruik van indirect optellen leidde tot gemengde resultaten. De eerste studies die het gebruik van verschillende rekenstrategieën in beeld trachtten te brengen door kinderen te vragen hoe ze te werk gegaan waren, toonden aan dat indirect optellen zelden werd gebruikt door zeven- tot negenjarigen (Blöte et al., 2001; Heinze et al., 2009; Selter, 2001). Meer recente studies in Nederland (Hickendorff, 2020) en Vlaanderen (Torbeyns et al., 2018) maakten gebruik van een keuze/geen-keuzemethode om het gebruik van indirect optellen te onderzoeken. Die methode houdt in dat de kinderen drie reeksen aftrekopgaven aangeboden krijgen: één reeks in een keuzeconditie, waarin ze voor elke opgave mochten kiezen of ze gebruikmaakten van direct aftrekken of indirect optellen, één reeks in een geen-keuzeconditie waarin ze alle opgaven verplicht met direct aftrekken moesten oplossen, en één reeks in een geen-keuzeconditie waarin ze alle opgaven verplicht met indirect optellen moesten oplossen. De resultaten van deze studies toonden aan dat kinderen indirect optellen weldegelijk kunnen toepassen, en zelfs enorm efficiënt zijn met deze strategie. Een grondige, systematische studie naar het gebruik van indirect optellen bij kinderen van verschillende leeftijden ontbrak echter nog aan het begin van mijn promotieonderzoek. Daarom was mijn eerste doel om het gebruik van deze strategie in beeld te brengen, en meer specifiek om te kijken naar de volgende vier strategieparameters: repertoire, frequentie, efficiëntie, en adaptiviteit. Strategierepertoire omvat het totaal aan strategieën die iemand kent om een taak op te lossen. Strategiefrequentie verwijst naar hoe vaak elk van die strategieën wordt toegepast. Efficiëntie is de accuraatheid en snelheid waarmee elke strategie wordt uitgevoerd, en, zoals eerder besproken, omvat strategieadaptiviteit het aanpassen van de strategiekeuzes aan de numerieke karakteristieken van de gegeven rekenopgaven.

Rekenonderzoekers buigen zich niet enkel over het gebruik van rekenstrategieën, maar ook over de samenhang ervan met bepaalde wiskundige principes. Sommige onderzoekers (Baroody et al., 2009; Selter, 2001) hebben gesuggereerd dat voor het gebruik van de indirecte optelstrategie inzicht in de inverse relatie vereist is. Kennis van dit principe betekent dat men begrijpt dat als ‘a + b = c’, dan ‘c – b = a’ en ‘c – a = b’. Immers, om gebruik te kunnen maken van indirect optellen om een bepaalde aftrekopgave, zoals bijvoorbeeld ‘a – b = ?’, op te lossen, moet een kind begrijpen dat het verschil voor deze opgave bepaald kan worden door bij de aftrekker op te tellen tot het aftrektal is bereikt; dus ‘b + ? = a’. Hoewel het verband tussen de inverse relatie en het gebruik van indirect optellen evident lijkt, werd deze nog nooit onderzocht. Daarom was mijn tweede doel om de associaties te onderzoeken tussen de kennis van kinderen van de inverse relatie, en de frequentie en adaptiviteit waarmee ze de indirecte optelstrategie toepassen.

Het frequent, efficiënt en adaptief gebruik van indirect optellen

In de eerste studie van mijn promotieonderzoek (Van Der Auwera et al., 2022) onderzocht ik of 151 tien- tot twaalfjarigen met verschillende wiskundige vaardigheidsniveaus indirect optellen toepassen voor het oplossen van aftrekopgaven en, indien ja, hoe frequent, efficiënt en adaptief ze dat doen. De kinderen uit deze studie kregen drie reeksen meercijferige aftrekopgaven aangeboden die ze mochten oplossen in een keuzeconditie, waarin ze voor elke opgave mochten kiezen of ze gebruikmaakten van direct aftrekken of indirect optellen, en twee geen-keuze condities. In één geen-keuzeconditie moesten ze alle opgaven oplossen met direct aftrekken, en in de andere geen-keuzeconditie moesten ze alle opgaven oplossen met indirect optellen. Strategierepertoire, -frequentie en -adaptiviteit werden onderzocht in de keuzeconditie, en strategie-efficiëntie werd bepaald in de geen-keuzecondities. De reeksen meercijferige aftrekopgaven bestonden voor de helft uit items met een klein verschil, bijvoorbeeld 504 − 476 = 28, waarvoor indirect optellen de meest adaptieve strategie is, en voor de andere helft uit items met een groot verschil, bijvoorbeeld 616 − 28 = 588, waarvoor direct aftrekken de meest adaptieve strategie is. De resultaten uit de keuzeconditie wezen uit dat een groot deel van de kinderen (77%) indirect optellen in hun strategierepertoire hadden, en dat de strategie werd gebruikt om iets minder dan de helft van de aangeboden aftrekopgaven op te lossen. Daarnaast werd indirect optellen in de geen-keuzecondities zowel accurater als sneller toegepast dan direct aftrekken. Dit grote voordeel in efficiëntie voor indirect optellen was echter volledig te wijten aan de accuraatheid en snelheid gemeten op de items met een klein verschil. Voor de items met een groot verschil werd geen verschil in efficiëntie gevonden tussen de twee strategieën. De resultaten van de keuzeconditie toonden ook dat bijna de helft van de kinderen adaptief waren in hun strategieselectie, en dus indirect optellen gebruikten voor het oplossen van items met een klein verschil, en direct aftrekken gebruikten voor het oplossen van items met een groot verschil. Het belang van deze resultaten mag niet onderschat worden, aangezien deze aantonen dat een strategie die niet/nauwelijks aan bod komt in de wiskundelessen, zijnde indirect optellen, frequent en adaptief wordt toegepast, en zelfs efficiënter is dan de standaard aangeleerde directe aftrekstrategie. Deze studie toont ook aan dat deze opmerkelijke resultaten voorkomen in alle leeftijdsgroepen, dus zowel in de tien-, elf- als twaalfjarigen.

De tweede studie (Van Der Auwera et al., 2023) bouwt voort op de bovenstaande resultaten. In deze studie onderzocht ik het gebruikt van indirect optellen in een groep nog jongere kinderen, namelijk 66 negenjarigen met verschillende wiskundige vaardigheidsniveaus. De kinderen kregen opnieuw drie reeksen meercijferige aftrekopgaven aangeboden in één keuzeconditie en twee geen-keuzecondities. Ditmaal bestonden de opgavenreeksen echter uit tweecijferige aftrekopgaven, waarvan de helft een klein verschil had (93 – 86 = 7), en de andere helft een groot verschil had (54 – 6 = 48). De resultaten van de keuzeconditie toonden dat bijna de helft van de kinderen (42%) indirect optellen in hun strategierepertoire hadden, en dat de strategie werd gebruikt om een kwart van de aangeboden aftrekopgaven op te lossen. Verder was de niet-onderwezen indirecte optelstrategie in de geen-keuzecondities even accuraat en snel als direct aftrekken voor het oplossen van aftrekopgaven met een klein verschil. Tenslotte ontdekte ik in de keuzeconditie dat één op vijf kinderen adaptief waren in hun strategieselectie, en dus indirect optellen gebruikten voor het oplossen van items met een klein verschil, en direct aftrekken gebruikten voor het oplossen van items met een groot verschil. Ook deze studie toont dus dat, zelfs al bij deze jonge kinderen, de indirecte optelstrategie een waardevolle, alternatieve rekenstrategie is.

Het belang van de inverse relatie voor indirect optellen

In de derde studie (Van Der Auwera et al., 2024) werden de associaties tussen de kennis van kinderen van de inverse relatie en de frequentie en adaptiviteit waarmee ze indirect optellen toepassen onderzocht. De frequentie en adaptiviteit van indirect optellen mat ik op dezelfde manier als in de vorige studies, ditmaal bij 57 elfjarigen. De kennis van de inverse relatie bracht ik in beeld aan de hand van twee taken: een terugkijktaak en een lettertaak. In de terugkijktaak kregen de kinderen een formulier met een reeks tweecijferige aftrekopgaven. Deze opgaven stonden steeds per twee onder elkaar genoteerd, en het correcte antwoord voor de bovenste opgave was steeds gegeven, terwijl dit niet het geval was voor de onderste opgave. Voor sommige duo’s kon de oplossing op de onderste opgave, bijvoorbeeld ‘91 – 43 = ?’, afgeleid worden van de bovenste opgave, 43 + 48 = 91, door gebruik te maken van de inverse relatie. Voor andere duo’s was dit echter niet het geval. Het antwoord op ‘18 + 42 = ?’ kan bijvoorbeeld niet afgeleid worden van de gegeven opgave ‘42 – 24 = 18’. De taak van de kinderen was om voor elk duo aan te geven of de oplossing op de onderste opgave afgeleid kon worden van de bovenste opgave. Naast de terugkijktaak maakte ik ook gebruik van de lettertaak, een taak die al in eerder onderzoek (Yip et al., 2022) gebruikt was om de kennis van kinderen van de inverse relatie te meten. In de lettertaak kregen de kinderen steeds één opgave bestaande uit letters, zoals bijvoorbeeld ‘H − C = F’, en moesten ze voor enkele afgeleide opgaven aangeven of deze correct, bijvoorbeeld ‘C + F = H’, of incorrect,  bijvoorbeeld ‘C + H = F’ of ‘C − H = F’, waren afgeleid op basis van de inverse relatie. In tegenstelling tot mijn verwachtingen, toonden de resultaten van dit onderzoek aan dat er geen associatie bestond tussen de frequentie waarmee de kinderen indirect optellen gebruikten en de scores op de taken die hun kennis van de inverse relatie maten. Ik ontdekte wel dat de scores op de terugkijktaak en de lettertaak samenhingen met het aantal adaptieve strategiekeuzes die de kinderen maakten. Meer kennis van de inverse relatie gaat dus samen met meer adaptieve strategiekeuzes.

Conclusie en aanbevelingen voor het rekenonderwijs

De resultaten van mijn promotieonderzoek tonen dat Vlaamse tien- tot twaalfjarigen, en in beperkte mate zelfs negenjarigen, frequent, efficiënt en adaptief gebruikmaken van indirect optellen voor het oplossen van aftrekopgaven. Dit is verbazingwekkend, gegeven dat er in het rekenonderwijs bijna geen aandacht wordt besteed aan deze strategie. Tenslotte wezen de resultaten van mijn promotieonderzoek ook op het belang van wiskundige conceptuele kennis voor het gebruik van rekenstrategieën. Zo ontdekte ik een samenhang tussen kennis van de inverse relatie en het adaptief gebruik van indirect optellen.

In het verleden hebben auteurs op basis van hun empirische onderzoeksresultaten reeds gepleit voor meer aandacht voor indirect optellen in het elementair wiskundeonderwijs (Hickendorff, 2020; Torbeyns et al., 2018). Dit pleidooi wordt ondersteund door de resultaten van mijn studies (Van Der Auwera et al., 2022, 2023), waaruit blijkt dat kinderen in de bovenbouw van het basisonderwijs zonder eerdere instructies deze strategie frequent, efficiënt en adaptief kunnen toepassen. Mijn resultaten suggereren bovendien dat het aanbieden van indirect optellen als alternatief voor direct aftrekken al bij negenjarigen van start kan gaan. Als afbeelding 1 voeg ik enkele opgaven met grote en kleine verschillen toe die, volgens de resultaten uit mijn studies, respectievelijk, het gebruik van direct aftrekken en indirect optellen uitlokken. Leerkrachten kunnen deze opgaven gebruiken om indirect optellen, naast direct aftrekken, te introduceren.

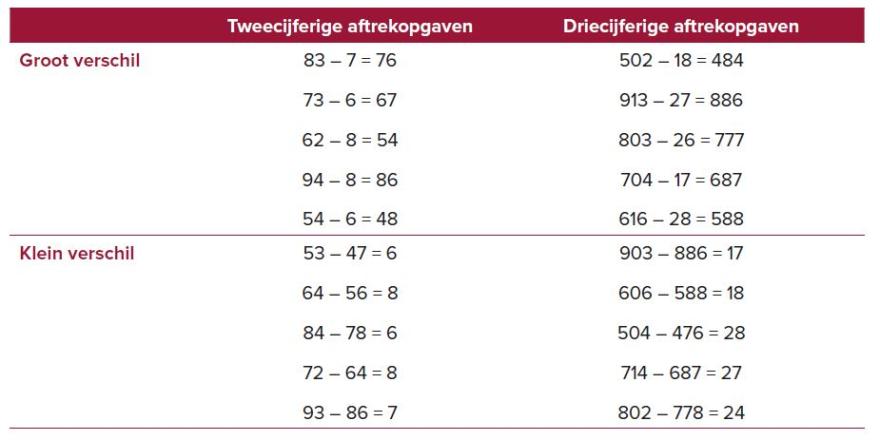
Het is echter van belang om niet enkel te focussen op indirect optellen, naast direct aftrekken, maar om actief te streven naar voldoende aandacht voor verschillende rekenstrategieën en het adaptief gebruik ervan. Recent onderzoek heeft uitgewezen dat de opkomst en ontwikkeling van nieuwe strategieën, en het adaptief leren gebruiken van deze strategieën, het best wordt ondersteund in een leeromgeving die maximaal inzet op het vergelijken van verschillende strategieën (Nemeth et al., 2021). Dit kan door kinderen een opgave meerdere keren te laten oplossen, steeds met een verschillende strategie, bijvoorbeeld met zowel direct aftrekken als indirect optellen, en daarna te bespreken wat de voor- en nadelen zijn van elke strategie. De vergelijking in afbeelding 2 toont bijvoorbeeld hoe kinderen bijvoorbeeld kunnen leren dat voor opgaven met een klein verschil indirect optellen een meer adaptieve strategie is dan direct aftrekken.

De bevinding dat de kennis van kinderen van de inverse relatie verband houdt met hun strategieadaptiviteit suggereert dat het nuttig kan zijn om in de rekenlessen aandacht te besteden aan dit principe. Een manier om dat te doen is om, zoals in de terugkijktaak, kinderen te confronteren met rijtjes rekensommen waarbij het juiste antwoord te vinden is door naar de vorige opgave te kijken, zoals bijvoorbeeld ‘43 + 48 = ?’ gevolgd door ‘91 − 43 = ?’, en daarna in een klasgesprek de achterliggende inverse relatie te bespreken. Als afbeelding 3 voeg ik een reeks met verwante optel- en aftrekopgaven toe die daarvoor gebruikt kunnen worden. Echter, verder onderzoek is nodig om de effectiviteit van dergelijke taken op het adaptief gebruik van indirect optellen na te gaan.

[1] Dit promotieonderzoek werd uitgevoerd onder de begeleiding van Bert De Smedt, Joke Torbeyns, en Lieven Verschaffel.