Creatief denken in het reken-wiskundeonderwijs

In dit artikel worden de resultaten van deze studies beschreven en vertaald naar aanbevelingen voor de onderwijspraktijk. Het onderzoek toont aan dat creatief denken bijdraagt aan prestaties op rekentaken, met name wanneer deze taken meerdere oplossingen hebben. Daarnaast blijkt het mogelijk om aspecten van creatief denken bij leerlingen te verbeteren in het reken-wiskundeonderwijs.

Waarom is creatief denken belangrijk?

In discussies omtrent onderwijs is veel aandacht voor welke vaardigheden leerlingen nodig hebben om goed voorbereid te zijn op de toekomst in een snel veranderende wereld. Deze vaardigheden worden ook wel 21e eeuwse vaardigheden genoemd en het gaat dan bijvoorbeeld om kritisch denken, maar ook creatief denken wordt genoemd (Thijs et al., 2014). De term 21e eeuwse vaardigheden is enigszins misleidend, want vaardigheden zoals creatief denken zijn natuurlijk altijd al belangrijk geweest in verschillende domeinen, zoals rekenen-wiskunde. Alhoewel veel mensen bij de term creativiteit eerder denken aan kunstvakken zoals tekenen, is creatief denken juist essentieel bij rekenen-wiskunde. Creatief denken helpt je namelijk om rekenproblemen op te lossen waarvoor je niet meteen een antwoord of strategie paraat hebt. Wiskundigen gebruiken creatief denken bijvoorbeeld om innovatieve oplossingen te bedenken, zoals de voorloper van de computer die wiskundige Alan Turing bedacht om versleutelde berichten van de Duitsers in de Tweede Wereldoorlog te ontcijferen (Hodges, 1983). Maar ook voor leerlingen op de basisschool is creatief denken essentieel. Creatief denken helpt leerlingen namelijk om bestaande kennis te integreren met nieuwe informatie en zo tot nieuwe ideeën te komen, wat essentieel is tijdens het leren (Montag-Smit & Maertz Jr., 2017).

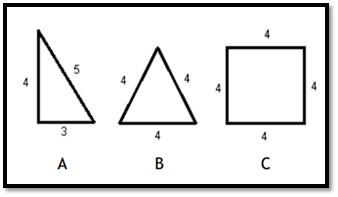
Bij rekenen-wiskunde staat het oplossen van verschillende problemen centraal (Schoenfeld, 2014). Met name bij nieuwe problemen waarvoor leerlingen niet meteen de juiste strategie of oplossing weten, helpt creatief denken hen om tot verschillende oplossingsmethoden te komen (Leikin, 2009). Leerlingen doen dit door te bepalen wat de belangrijkste elementen zijn van het rekenprobleem en hun bestaande kennis te activeren. Wanneer zij die kennis en informatie flexibel gebruiken, kunnen zij een oplossingsmethode voor het probleem bedenken (Hadamard, 1996; Mann, 2005). Een voorbeeld van zo’n opgave is om leerlingen te vragen een vierkant op zoveel mogelijk verschillende manieren in vier gelijke stukken te verdelen en op zoek te gaan naar originele oplossingen (afbeelding 1). Door creatief te denken, komen leerlingen ook tot meer originele oplossingen. Niet elk rekenprobleem is natuurlijk nieuw voor leerlingen. Toch helpt creatief denken hen ook wanneer zij de oplossingsmethode al paraat hebben. Door verschillende (originele) oplossingsmethoden te bedenken en te vergelijken, leren leerlingen namelijk wiskundige concepten beter te begrijpen (Kattou et al., 2013; Leikin, 2007; Mann, 2006).

Originaliteit is een belangrijk element van creativiteit, maar niet het enige criterium. Wanneer een leerling een originele oplossingsmethode bedenkt voor een rekenprobleem die uiteindelijk een fout antwoord oplevert, kan dit niet als creatief worden gezien. In creativiteitsonderzoek wordt creativiteit daarom ook wel omschreven als de ‘interactie tussen vaardigheid, proces en omgeving die leidt tot een product dat zowel nieuw als nuttig is zoals bepaald in een specifieke context’ (vrij vertaald uit Plucker et al., 2004, p. 90). Voor leerlingen in het reken-wiskundeonderwijs betekent dit dat hun oplossingen of ideeën die origineel en nuttig zijn binnen de context van het reken-wiskundeonderwijs als creatief kunnen worden gezien. Overigens betekent de inschatting van creativiteit in een bepaalde context ook dat je creatief denken als relatief kan beschouwen. Ideeën hoeven niet origineel te zijn binnen het domein van wiskunde als geheel, maar origineel voor de specifieke leerling of groep leerlingen.

Alhoewel er nog niet veel onderzoek is gedaan naar het stimuleren van creativiteit in het reken-wiskundeonderwijs, is er wel onderzoek gedaan waaruit blijkt dat kinderen die beter zijn in creatief denken, ook vaak betere rekenprestaties laten zien (Bicer, 2021). Daarnaast is aangetoond dat creativiteit als vaardigheid niet in beton gegoten is. Het is mogelijk om deze vaardigheid te trainen (Scott et al., 2004). Met deze onderzoeksuitkomsten en de eerder genoemd aandacht voor toekomstbestendig onderwijs groeit ook de aandacht voor creatief denken in het Nederlandse onderwijs. In de plannen voor de curriculumvernieuwing van het primair onderwijs is creatief denken bijvoorbeeld opgenomen als vakoverstijgende vaardigheid die leerlingen onder de knie moeten krijgen (Curriculum.nu, 2018; Van Zanten & Schmidt, 2023). Om creatief denken echter goed te integreren in het reken-wiskundeonderwijs is het belangrijk om te weten welke creatieve denkvaardigheden kinderen nu echt helpen om rekenproblemen op te lossen en hoe we creatief denken binnen de context van het reken-wiskundeonderwijs goed kunnen stimuleren. Het ondersteunen van creatief denken zou er in verschillende domeinen namelijk anders uit kunnen zien, omdat creatief denken naast algemene componenten ook vakspecifieke componenten bevat.

Meer specifiek veronderstelt de Amusement Park Theory (Baer & Kaufman, 2005) dat mensen verschillen in de mate waarin zij algemeen creatief potentieel hebben (bijvoorbeeld omdat mensen verschillen in motivatie en intelligentie). Dat algemene potentieel kan in verschillende domeinen, zoals bijvoorbeeld rekenen-wiskunde, worden ingezet, waarvoor ook kennis van het specifieke domein nodig is. In het promotieonderzoek (De Vink, 2023) hebben we ons gericht op twee creatieve denkvaardigheden die hun basis kennen in theorie over intelligentie: divergent en convergent denken (Guilford, 1973). Bij divergent denken gaat het om het bedenken van verschillende oplossingen of antwoorden voor een bepaald probleem, terwijl het bij convergent denken gaat om het evalueren van deze opties en het kiezen van de best mogelijke oplossing of oplossingsmethode. Eerder onderzoek naar creatief denken heeft bijna uitsluitend gefocust op creatief denken als geheel of alleen op divergent denken, in plaats van de verschillende vaardigheden die leerlingen inzetten tijdens een creatief denkproces. Om divergent en convergent denken te meten is gebruik gemaakt van zowel meer algemene taken van creativiteit als taken die gericht zijn op creativiteit specifiek binnen het domein rekenen-wiskunde. Op deze manier kan recht worden gedaan aan zowel de domein-algemene als domein-specifieke elementen van creativiteit (Baer & Kaufman, 2005).

In het onderzoek is geprobeerd om twee hoofdvragen te beantwoorden: 1) Welke rol spelen divergent en convergent denken bij het oplossen van rekenen-wiskunde problemen door basisschoolleerlingen? 2) Hoe kunnen divergent en convergent denken succesvol worden ondersteund bij het oplossen van reken-wiskundeproblemen door basisschoolleerlingen? Deze twee hoofdvragen zijn onderzocht in drie verschillende studies, die zijn uitgevoerd in groep 7 van het regulier basisonderwijs.

Rekentaken met meerdere oplossingen vragen om creativiteit

In de eerste studie in het onderzoek (De Vink et al., 2022a) is onderzocht hoe divergent en convergent denken samenhangen met verschillende typen rekentaken. In deze studie zijn divergent denken en convergent denken gemeten met twee domein-algemene taken om zicht te krijgen op de samenhang van domein-algemene creativiteit met rekenvaardigheid. We maakten gebruik van verbale en visuele taken om zo volledig mogelijk zicht te krijgen op de creatieve denkvaardigheid van leerlingen. Bij de verbale taken ging het om het opschrijven van verschillende originele manieren om een kartonnen doos te gebruiken (divergent denken) of het kiezen van een woord dat paste bij drie andere woorden (convergent denken). Op de visuele taak ging het om het maken van verschillende tekeningen met één vorm (divergent denken), of maken van één tekening met meerdere verschillende vormen (convergent denken). In afbeelding 2 staan de verschillende vormen die in de convergente tekening konden worden gebruikt. Deze tekeningen werden bijvoorbeeld beoordeeld op aanwezigheid van een thema of verhaal. Zulke taken geven een inzicht in het vermogen van kinderen om verschillende ideeën te bedenken, of juist ideeën te selecteren en evalueren. Prestaties op deze taken zijn gerelateerd aan de reken-wiskunde prestaties van leerlingen op een taak met vragen waarbij telkens één correct antwoord was en een taak waarbij leerlingen juist zoveel mogelijk antwoorden moesten geven. De taak met vragen met één correct antwoord die we gebruikten was de Cito LVS 3.0 toets. De taak met meerdere goede antwoorden kwam uit het onderzoek van Kattou et al. (2013) en bestond uit drie vragen waarbij leerlingen telkens geïnstrueerd werden om zoveel mogelijk verschillende en originele antwoorden te bedenken. Afbeelding 3 toont een voorbeeld van een dergelijke vraag.

Uit de analyses bleek dat vooral convergent denken samen hing met rekenvaardigheid. Kinderen die goed waren in convergent denken op de verbale taak presteerden namelijk beter op zowel de rekentaak met één oplossing als de rekentaak met meerdere oplossingen. Bij convergent denken gaat het vooral om het evalueren en selecteren van ideeën. Dit ligt dicht bij processen zoals logisch redeneren en geautomatiseerde/gememoriseerde rekenkennis inzetten, wat leerlingen op zowel taken met één als met meerdere oplossingen helpt (Cropley, 2006; Tabach & Levenson, 2018). Als je een rekenprobleem krijgt aangeboden helpt convergent denken je namelijk om te selecteren welke bestaande rekenkennis of geleerde strategieën bij dit probleem passen en de beste kans op één of meerdere oplossingen bieden. Bij divergent denken gaat het daarentegen juist om het bedenken en creëren van verschillende opties. De rol van divergent denken was afhankelijk van hoe goed kinderen convergent konden denken en verschilde per taak. Op de taak waarbij telkens om één goede oplossing werd gevraagd presteerden kinderen die goed waren in verbaal convergent denken, maar niet goed in verbaal divergent denken het beste. Omdat op deze taak (de Cito LVS toets) vooral rekenproblemen worden gebruikt die kinderen met bestaande kennis en procedures op kunnen lossen is divergent denken hiervoor minder belangrijk (Schoenfeld, 2014). Daarnaast lijkt de taak die we gebruikten voor verbaal convergent denken het meeste op de (veelal verbale) taken die op school al worden gebruikt, ook bij rekenen. Daardoor laten de kinderen die goed zijn in deze verbale taak van creatief denken over het algemeen ook hogere rekenprestaties zien.

Op de taak met meerdere goede oplossingen presteerden juist kinderen die goed waren in visueel divergent denken én visueel convergent denken het beste. Naast het selecteren en evalueren van ideeën is het bij een dergelijke taak die voor kinderen meestal vrij nieuw is heel belangrijk dat kinderen ook meerdere verschillende strategieën en antwoorden kunnen bedenken (Tabach & Levenson, 2018). Omdat de taak met meerdere oplossingen nieuw(er) is voor leerlingen speelt visuele creativiteit mogelijk een grotere rol dan verbale creativiteit. Nieuwe rekentaken maken lijkt namelijk in hogere mate een beroep te doen op visuele vaardigheden dan bestaande of bekende rekentaken maken, bijvoorbeeld omdat kinderen bij nieuwe taken meer gebruik maken van visuele representaties van rekenkundige concepten (Zmigrod et al., 2015; Van de Weijer-Bergsma et al., 2015). Alhoewel creatief denken dus samenhing met beide soorten rekentaken, bieden rekentaken met meerdere oplossingen waarschijnlijk meer mogelijkheden om creatief denken in te zetten omdat er verschillende denkvaardigheden worden gevraagd.

Leerlingen vinden creatief denken niet makkelijk

In de hiervoor beschreven studie is gekeken naar prestaties op verbale en visuele taken van divergent en convergent denken om inzicht te krijgen in de (algemene) creatieve denkvaardigheid van leerlingen en hoe deze samenhangt met reken-wiskundeprestaties. Het is echter ook heel belangrijk om inzicht te krijgen in het creatieve denkproces van leerlingen op een domein-specifieke creativiteitstaak. Dit is gedaan in de tweede studie van dit proefschrift (De Vink et al., 2022b). Welke denkstappen maken leerlingen nu precies wanneer hen wordt gevraagd om een (creatieve) rekentaak te maken? Theoretische modellen (bijvoorbeeld Lubart, 2018) beschrijven dat dit denkproces bestaat uit afwisselende stappen van divergent en convergent denken. De vraag is echter of dit ook voor het domein rekenen-wiskunde het geval is. Om hier zicht op te krijgen zijn is er individueel onderzoek gedaan met een groep leerlingen. Omdat individuele verschillen tussen leerlingen invloed zouden kunnen hebben op hun creatieve denkproces is gekozen voor een diverse groep leerlingen bestaande uit sterke en zwakke rekenaars. Leerlingen die aan de eerste studie hadden meegedaan en wiens rekenscores bij de hoogste of laagste 15% van de steekproef scoorden, werden geselecteerd als sterke of zwakke rekenaar voor dit onderzoek. Deze leerlingen maakten twee reken-wiskunde taken die beiden meerdere oplossingen hadden. De eerste taak was een taak waarbij leerlingen zelf verschillende reken-wiskunde opgaven moesten bedenken aan de hand van een plaatje. Bij de tweede taak moesten leerlingen verschillende sommen bedenken met dezelfde uitkomst, waarbij zij een aantal getallen en operatoren kregen aangereikt. Bij beide taken werd leerlingen gevraagd om hardop te denken aan de hand van verschillende vragen, bijvoorbeeld ‘hoe ben je op dit idee gekomen?’, om zo inzicht te krijgen in hun creatieve denkproces. Het gesprek tussen kind en testleider werd opgenomen en uitgeschreven. Deze uitgeschreven tekst vormde samen met de antwoorden van leerlingen op de rekentaken het uitgangspunt voor de analyse.

In de analyse werd bepaald of de ideeën die kinderen bedachten creatief waren en hoe het creatieve denkproces verliep. Ideeën werden geselecteerd als creatief wanneer zij passend waren voor de taak, maar ook origineel. Uit de resultaten bleek dat zowel sterke als zwakke rekenaars moeite hadden met het bedenken van creatieve ideeën. De meeste ideeën leken sterk op de ideeën die de kinderen al eerder hadden bedacht en werden beoordeeld als niet creatief. Wanneer kinderen creatieve ideeën bedachten, gebruikten ze hier voornamelijk en soms zelfs uitsluitend divergent denken voor. Soms bleek het lastig om divergent en convergent denken van elkaar te onderscheiden en hingen beide denkprocessen sterk met elkaar samen. Daarom is tijdens het codeerproces een categorie toegevoegd: de combinatie van divergent en convergent denken. De meest originele ideeën werden bedacht door kinderen die divergent denken afwisselden of combineerden met convergent denken. Sterke rekenaars gebruikten vaker convergent denken en combinaties van divergent en convergent denken. In overeenstemming met theoretische modellen wisselden kinderen inderdaad vaak af tussen verschillende stappen van divergent en convergent denken. Dit betekende dat leerlingen een cyclisch denkproces lieten zien. Na verschillende mogelijke oplossingen te hebben bedacht, gingen leerlingen deze opties beoordelen en de meest kansrijke verder uitwerken. Daar stopte het proces echter niet, want na deze beoordeling werden er weer nieuwe ideeën bedacht en beoordeeld. Dit proces herhaalde zich vaak een aantal keer.

Je kunt creatief denken bij rekenen-wiskunde verbeteren

Het feit dat de meeste ideeën niet als creatief konden worden beschouwd laat zien dat creatief denken niet vanzelf gaat en dat het belangrijk is om leerlingen hierbij te ondersteunen. In de derde studie van dit proefschrift is daarom onderzocht hoe divergent en convergent denken kunnen worden ondersteund tijdens de reken-wiskundeles (De Vink et al., 2023). In dit onderzoek hebben we ons specifiek gericht op het domein meetkunde en ondersteuning van domein-specifiek creatief meetkundig denken. In het Nederlandse reken-wiskundeonderwijs krijgt meetkunde relatief minder aandacht dan andere wiskundige domeinen. Meetkundige problemen zijn daardoor gemiddeld nieuwer voor leerlingen en bieden meer mogelijkheden voor creatief denken (Haavold, 2020). Leerdoelen op het gebied van meetkunde zijn bijvoorbeeld het kunnen creëren van een mozaïekpatroon en hierover redeneren (Noteboom et al., 2017). Voor dit onderzoek ontwikkelde een team van (vakdidactisch) onderzoekers een lessenserie van vijf lessen waarin bestaande doelen op het gebied van meetkunde werden geïntegreerd met leerdoelen op het gebied van creatief denken, bijvoorbeeld ‘de leerling kan op een creatieve manier een patroon maken met gekleurde tegels’. Zodoende nodigden de lessen uit om creatief te denken. Voor deze lessen werd gebruik gemaakt van materialen uit het Meetkunst-project (Schoevers, 2019), evenals de Grote Rekendag (Keijzer & Kuijpers, 2007). De vijf ontworpen lessen duurden 60 minuten en werden in één week elke dag aan deelnemende klassen aangeboden.

De lessenserie ging specifiek om een meetkundige benadering van patronen. Elke les werd er gestart met een klassikale introductie van het onderwerp dat in die les centraal stond, bijvoorbeeld symmetrie en spiegeling. Daarna gingen leerlingen aan de slag met een opdracht in duo’s, bijvoorbeeld het ontwerpen van een patroon met behulp van spiegels. Na de opdracht werd klassikaal besproken wat leerlingen tijdens de opdracht hadden ontdekt. Elke deelnemende klas volgde dezelfde les, maar de ondersteuning die leerlingen kregen tijdens de les verschilde tussen klassen. Elke klas werd toegewezen aan één van drie groepen: 1) een groep waarin geen ondersteuning werd geboden voor creatief denken, 2) een groep met gedeeltelijke ondersteuning waarin alleen het divergent denken werd ondersteund, 3) een groep met volledige ondersteuning waarin het divergent en convergent denken werd ondersteund. Divergent denken werd ondersteund door middel van een individuele brainstorm oefening. Voordat leerlingen in duo’s aan de opdracht begonnen werden zij gevraagd om na te denken over zoveel mogelijk verschillende (en originele) manieren om de opdracht aan te pakken. De bedachte ideeën konden ze daarna in hun duo bespreken. Convergent denken werd ondersteund door te oefenen met het evalueren en selecteren van ideeën. Bij het ontwerpen van een patroon met spiegels werden leerlingen bijvoorbeeld aangespoord om nog eens naar hun ideeën te kijken nadat zij herinnerd waren aan het doel van de opdracht. Leerlingen werd gevraagd om te bepalen welke ideeën zij het meest origineel en passend bij de taak vonden. Los van het creatief denken werd in alle groepen het meetkundig denken ondersteund, bijvoorbeeld wanneer leerlingen moeite hadden met het concept symmetrie.

Middels een voor- en nameting werd de ontwikkeling van de meetkundevaardigheid, divergente denkvaardigheid en convergente denkvaardigheid in kaart gebracht. Divergent en convergent denken werden gemeten met domein-specifieke taken. Voor divergent denken ging het om het bedenken van verschillende antwoorden voor meetkundige problemen, waarbij werd gelet op de hoeveelheid antwoorden, verscheidenheid van antwoorden en originaliteit van de antwoorden. Voor convergent denken ging het om het beoordelen van verschillende meetkundige ideeën. Meer specifiek beoordeelden kinderen hoe origineel zij verschillende meetkundige ideeën vonden. Creativiteitsexperts beoordeelden deze ideeën ook. Hoe meer het oordeel van kind en expert overeenkwam, hoe hoger de score voor convergent denken. Uit een analyse van deze gegevens bleek dat leerlingen, ongeacht de soort ondersteuning die zij ontvingen, na de vijf lessen niet beter presteerden op het gebied van convergent denken en meetkundevaardigheid. Mogelijk is het convergent denken niet toegenomen omdat leerlingen hier al vrij goed in waren getuige de relatief hoge prestaties op de voormeting. Overigens was op het gebied van meetkunde een kleine verbetering zichtbaar, maar deze was niet significant. Leerlingen presteerden echter wel beter op het gebied van divergent denken. In de groep met volledige ondersteuning lukte het leerlingen na de vijf lessen beter om meerdere antwoorden te bedenken. In de groep met geen of gedeeltelijke ondersteuning lukte het leerlingen beter om gevarieerde en originele antwoorden te geven. Dit laat zien dat de lessen die in het onderzoek zijn ingezet, al dan niet in combinatie met ondersteuning, kunnen bijdragen aan verbeteringen in aspecten van creatief denken. Verder onderzoek is echter nodig om te bepalen hoe divergent denken, convergent denken en rekenvaardigheid gezamenlijk ondersteund kunnen worden, bijvoorbeeld middels een langer lestraject.

Aanbevelingen voor de onderwijspraktijk

Al met al laat dit onderzoek zien dat creatief denken belangrijk is bij rekenen-wiskunde. Zowel divergent als convergent denken blijkt samen te hangen met rekenen-wiskunde, alhoewel beide denkvaardigheden anders worden ingezet. Divergent denken kan helpen om verschillende antwoorden of ideeën te bedenken, wat met name bij een rekentaak die meerdere oplossingen heeft belangrijk is. Convergent denken helpt om deze verschillende ideeën te evalueren en het meest geschikte idee te kiezen. Dit helpt bij taken die om één antwoord vragen, maar ook om tot originele ideeën te komen. Wanneer we kijken naar het creatieve denkproces op rekentaken met meerdere oplossingen, zien we dat kinderen die kunnen afwisselen tussen divergent en convergent denken het beste tot creatieve ideeën komen. Dat blijkt echter niet makkelijk. Zowel sterke als zwakke rekenaars bedenken met name niet-creatieve ideeën. Het is dus belangrijk om creatief denken in de rekenles te ondersteunen. Voor convergent denken blijkt dat nog niet makkelijk te zijn. Divergent denken daarentegen kan makkelijker ondersteund worden.

Aandacht schenken aan creatief denken betekent niet dat er weinig aandacht uit moet gaan naar een sterke rekenbasis en het automatiseren van bewerkingen, want zulke kennis helpt leerlingen juist om ook creatief te kunnen denken bij rekenen (Huang et al., 2017). Een goede balans tussen meer basale rekenvaardigheden en meer gevorderde rekenvaardigheden zoals creatief denken is essentieel. Aandacht voor creatief denken bij rekenen vraagt in ieder geval om een selectie van de juiste soort taak die voldoende ruimte biedt om creatief denken in te zetten. Een taak met meerdere oplossingen lijkt hiervoor een goede keuze omdat hierbij een beroep wordt gedaan op zowel divergent als convergent denken. Zulke taken zitten echter nog weinig in de bestaande rekenmethoden. De eerder benoemde materialen van het Meetkunst-project en de Grote Rekendag bieden hiervoor een uitkomst. Maar ook de taken die in dit onderzoek zijn gebruikt om creatief denken bij rekenen te meten zijn geschikt. Het gaat dan bijvoorbeeld om het verzinnen van meerdere antwoorden op de vraag welke vorm er niet bij hoort, het zelf verzinnen van rekenopgaven of het maken van zo veel mogelijk sommen met een gelijke uitkomst. Leerkrachten kunnen echter ook hun eigen creativiteit gebruiken om vergelijkbare taken te ontwerpen. Het is belangrijk dat een dergelijke taak meerdere oplossingen heeft, zodat leerlingen allerlei antwoorden kunnen geven, waaronder meer originele antwoorden.

Om het divergent denken van leerlingen op zo’n taak te ondersteunen kan een individuele brainstorm oefening worden ingezet. Het is bij zo’n oefening belangrijk dat leerlingen eerst in stilte zelf antwoorden bedenken, want dan worden zij minder geremd in het bedenken van ideeën door sociale processen zoals angst voor kritiek van klasgenoten (Nijstad & Stroebe 2006). Daarnaast is aandacht voor convergent denken belangrijk. Als leerlingen namelijk enkel gefocust zijn op het bedenken van zoveel mogelijk verschillende antwoorden is de kans groot dat daar ook foute of willekeurige antwoorden tussen zitten (Tabach & Levenson, 2018). Alhoewel de oefening voor convergent denken die in dit onderzoek is toegepast het convergent denken van leerlingen niet heeft verbeterd, kan het nog steeds nuttig zijn om deze in te zetten. Zo maken leerlingen namelijk kennis met een compleet creatief denkproces. Uiteindelijk helpt het oefenen met creatieve opdrachten leerlingen om rekenkundige concepten beter te begrijpen en de rekenontwikkeling te stimuleren, wat belangrijk is voor alle leerlingen (Beghetto, 2016).