Leren via probleemoplossen
Optellen en aftrekken van breuken
Kirschner et al. (2018) geven aan dat ontdekkend leren en probleemoplossen teveel vraagt van het werkgeheugen. Dat neemt niet weg dat ontdekkend leren en probleemoplossen centraal staan in de didactische aanpak die gebruikt wordt in hoogst scorende landen. Een analyse van het optellen van ongelijknamige breuken toont dat aanpakken die gebaseerd zijn op probleemoplossen voor leerlingen meer perspectief bieden dan het voordoen en nadoen, zoals bijvoorbeeld uitgewerkt in de EDI-aanpak.
Inleiding
In de aanhef van een artikel van Mostert en Hickendorff (2024) wordt Matthijs opgevoerd die hard aan zijn rekenopgaven werkt maar bij breuken vastloopt. Hij snapt er niets van: ‘Waarom is bij $\frac{3}{4}$ + $\frac{2}{5}$ het antwoord 1 $\frac{3}{20}$ en niet $\frac{5}{9}$?’
Kan Matthijs, met wat hulp, die vraag niet zelf beantwoorden?
Zijn leerlingen van groep 6/7 niet in staat om onder leiding van de leraar zelf de procedure van het optellen en aftrekken van ongelijknamige breuken te ontdekken?
Voorstanders van leren door middel van probleem oplossen via interactieve instructie (IPO) beantwoorden deze vraag bevestigend. Pleitbezorgers van expliciete directe instructie (EDI) daarentegen stellen probleemoplossen juist niet voorop, maar laten het op z’n best als sluitstuk van de les fungeren.
Twee basisfuncties van probleemoplossen
Zo rekenen Kirschner et al (2018) de activiteiten van ontdekkend leren en probleemoplossen zelfs tot twee van de tien didactische hoofdzonden.
Hun hoofdbezwaren tegen een en ander luiden als volgt:
‘Tijdens ontdekkend leren moeten zij steeds op zoek naar verbanden tussen zaken en de principes die van kracht zijn in het domein. Maar beginners hebben nauwelijks domeinkennis en geen systematische aanpak om te onderzoeken en experimenteren. Dit vergt daarom heel erg veel van hun werkgeheugen, te meer omdat onervaren leerlingen door onwetendheid niet alle elementen in het domein met elkaar in verband kunnen brengen. Zij krijgen te maken met een explosie van combinaties, zonder de kennis om die onder controle te houden. Bovendien resulteert deze belasting van het werkgeheugen niet in meer kennis in het langetermijngeheugen. Daarnaast drijft deze aanpak op de gedachte dat het kind een soort kleine wetenschapper is.’ (Kirschner et al, 2018, p. 157)
‘Laat ze eerst leren, dan begeleid oefenen, dan vrij oefenen, en misschien pas daarna zelf ontdekken’, aldus vatten Kirschner et al. hun standpunt samen.
Het leren van rekenfeiten, procedures en concepten wordt losgekoppeld van probleemoplossen dat volgens deze onderwijstheorie niet als basis ervan kan fungeren.
Deze onderwijspsychologische opvatting staat haaks op de vakdidactische visie die in de hoogst scorende landen van de wereld in praktijk wordt gebracht, zoals bijvoorbeeld in Japan en China.
Takahashi bijvoorbeeld schrijft over twee functies van probleemoplossen: (1) om kennis, begrippen en procedures te leren, (2) om leren problemen op te lossen.
‘In Japan problem solving is often viewed as a powerful approach for developing mathematical concepts and skills. Thus, Japanese teachers use developing problem-solving skills and strategies but also throughout the curriculum in order to develop mathematical concepts, skills and procedures.’ (Takabashi, 2019, p.3; zie ook Takabashi, 2021).
In de bijgevoegde Chinese videoles van Master MT-304 is te zien hoe die basisfunctie (1) via interactief probleemoplossend onderwijzen (IPO) bij optellen en aftrekken van ongelijknamige breuken in praktijk wordt gebracht[i] (Miao, Bokhove & Reynolds, 2024).
Om deze IPO-aanpak zo scherp mogelijk weer te geven, schetsen we eerst de contrasterende achtergrond ervan via een EDI-lessenserie[ii]
EDI-aanpak optellen ongelijknamige breuken
Laten we eens nagaan hoe basisfunctie (1) van probleem oplossen bij het opereren met ongelijknamige breuken kan worden ingezet dan wel genegeerd.
In de breukenleergang volgens de EDI-methode ‘Getal & Ruimte junior’ (2017) worden eerst het optellen en aftrekken van gelijknamige breuken, de gelijkwaardigheid van breuken plus het vergelijken en ordenen van ongelijknamige breuken uitgelegd en ingeoefend. Ieder onderdeel begint met een rekenrecept.
Bij de les over breuken vergelijken bijvoorbeeld luidt de uitleg in het leerlingenboek:
‘Om breuken te vergelijken moeten ze gelijknamig zijn.
Je zoekt daarvoor het kleinste getal dat in de tafel van de ene noemer 3 én de andere noemer 6 voorkomt.
$\frac{2}{3}$ < $\frac{5}{6}$ want $\frac{2}{3}$ = $\frac{4}{6}$.’
Leerlingen krijgen geen gelegenheid om zelf te ontdekken dat ze met de eerder opgedane kennis over gelijkwaardigheid die ongelijknamige breuken kunnen ordenen en vergelijken door ze gelijknamig te maken.
De eerste les over het optellen en aftrekken van ongelijknamige breuken opent de uitleg op dezelfde wijze met:
‘Om breuken op te tellen of af te trekken moeten ze gelijknamig zijn. $\frac{1}{2}$ + $\frac{1}{4}$ = $\frac{2}{4}$ + $\frac{1}{4}$, want $\frac{1}{2}$ = $\frac{2}{4}$.’
1. De leerkracht neemt het voortouw en laat via het leerboek aan de hand van een cirkeldiagram, rechthoek en strook zien hoe met een opdeling in vieren een dergelijke opgave in een som van gelijknamige breuken kan worden omgezet (Getal in Ruimte junior, 7A, p.60).
2. Met behulp van de eerder geleerde kennis van gelijkwaardige breuken lossen de leerlingen onder leiding van de leraar vervolgens samen nieuwe opgaven als $\frac{2}{3}$ + $\frac{1}{9}$ op.
3. Daarna worden aftreksommen als $\frac{7}{10}$ – $\frac{1}{6}$ zelfstandig in groepjes verwerkt en klassikaal nabesproken.
4. Vervolgens wordt een reeks soortgelijke opgaven door iedere leerling zelfstandig gemaakt.
5. En de les wordt afgesloten met een korte samenvatting.
De fasering van de les ziet er vanuit de leraar bezien zo uit:
‘ik – wij – jullie – jij – ik’
IPO-aanpak ongelijknamige breuken
In de IPO-fasering van geleid ontdekkend leren verwijst de eerste ‘ík’ in de genoemde trits niet naar de leraar maar naar de leerling die de vraag krijgt voorgelegd:
‘Hoeveel is $\frac{1}{2}$ + $\frac{1}{4}$?’
Uit groep 6/7 blijken hierop in de regel net als in Master MT-304 drie antwoorden naar voren te komen: $\frac{2}{6}$, $\frac{1}{3}$ en $\frac{3}{4}$. In de klassikale bespreking, ‘wij’, worden die van $\frac{2}{6}$ en $\frac{1}{3}$ verworpen, omdat beide uitkomsten kleiner zijn dan $\frac{1}{2}$, wat uiteraard niet kan. Voor het vervolg van de leergang is dit een cruciaal onderdeel waarin de vraag van Matthijs wordt beantwoord.
Vervolgens laten leerlingen op het bord zien hoe ze tot het juiste antwoord $\frac{3}{4}$zijn gekomen. Daarbij worden verschillende visuele modellen en getalsmatige voorstellingen gebruikt: cirkeldiagrammen, vierkanten, rechthoeken, getallenlijnen, strips, plus gelijkwaardige breuken die eerder al bij het vergelijken van ongelijknamige breuken dienst deden.
De algemene conclusie die uit dit modelvoorbeeld wordt getrokken luidt, dat bij optellen en aftrekken de breuken eerst gelijknamig gemaakt moeten worden.
In de volgende fase wordt deze rekenregel op andere opgaven toegepast, zoals $\frac{1}{2}$ + $\frac{1}{3}$ en $\frac{2}{3}$ + $\frac{1}{4}$. Ook kan ruimte worden geboden tot het ontwerpen van zelfbedachte sommen.
Tot slot wordt de les door de leraar afgesloten met een korte samenvatting van het geleerde plus eventueel een vooruitblik op het vervolg, namelijk het optellen en aftrekken van samengestelde breuken.
Dit voorbeeld van een onderzoekgerichte aanpak van breuken, die al sinds jaar en dag in het Nederlandse rekenonderwijs wordt gepropageerd, is zoals eerder opgemerkt, in de Chinese videoles MasterMT-304 waar te nemen. Deze verwijzing wordt hier niet toevallig gemaakt omdat, zoals gezegd, in de hoogst scorende landen van de wereld het leren via probleem oplossen tot de gangbare onderwijspraktijk behoort. (Zie bijvoorbeeld ook Isoda, 2010, en Kohn, 2024.).
Het belang van directe instructie als didactische werkvorm staat bij IPO uiteraard niet ter discussie. In bepaalde omstandigheden kan veelvuldige toepassing ervan zelfs praktisch noodzakelijk zijn. Deze derde weg volgt bij het optellen van ongelijknamige breuken de leraar die de leerlingen nadrukkelijk en veelvuldig in de uitleg betrekt, en daarbij alle genoemde visueel en numeriek onderbouwde argumenten aan bod laat komen – de route van de interactieve uitleg.
Algemene doelstellingen
Tot slot rijst de vraag wat in het voorbeeld van het leren optellen van ongelijknamige de meerwaarde van IPO ten aanzien van EDI is. De winst zal op korte termijn niet in de goedscores van de rekenvaardigheid te zien zijn. Tenminste niet als aan het inoefenen van de procedure in de ‘jij-fase’ van beide aanpakken evenveel aandacht wordt besteed.
Nogmaals: wat is dan de meerwaarde van IPO ten opzichte van EDI?
Deze kernvraag leidt ons naar de algemene doelstellingen van het (reken)onderwijs, waarvan naast de rekenkundige waarde ook de persoonlijke en sociale waarden een essentieel onderdeel vormen. Zelf en/of samen met anderen een rekenkundig kernprobleem oplossen zoals bijvoorbeeld het optellen van twee ongelijknamige breuken geeft meer plezier, voldoening en gevoel van eigenwaarde dan het navolgen van een (welbegrepen) rekenrecept door de leraar. En mede daardoor kan het ook een positieve reken-attitude en attitude t.o.v. het rekenen bevorderen – aldus luidt het uitgangspunt van de IPO-didactiek. Hetzelfde geldt voor de positieve invloed van (deels) zelf verworven inzichten op langere termijn als andere procedures met breuken worden geleerd[iii]
Slotsom
Het model van expliciete directe instructie (EDI) als didactisch systeem, biedt de leerlingen geen of weinig gelegenheid om zelf – onder didactische leiding van de leraar – kennis, vaardigheden, begrippen en inzichten te verwerven. Men gaat er daarbij vanuit dat kinderen daartoe niet zelf in staat zijn.
Interactief onderwijzen via probleemoplossen (IPO) benut de mogelijkheid van geleid ontdekkend leren nadrukkelijk wel. In dit opzicht komt deze vakdidactische opvatting overeen met die van een tweede richting in de onderwijspsychologie die eveneens het belang van onderzoekend leren benadrukt (De Jong et al., 2023).
[iii] Vermenigvuldigen en delen beginnen in G & R jr met de uitleg:
a). Bij het vermenigvuldigen van een heel getal met een breuk,
vermenigvuldig je de teller met dat getal.
7 x $\frac{1}{6}$ = $\frac{(7x1)}{6}$ = $\frac{7}{6}$ = 1 $\frac{1}{6}$
b). Bij het vermenigvuldigen van een breuk met een heel getal, vermenigvuldig je de teller met dat getal.
$\frac{1}{4}$ deel van 12 = 3
$\frac{1}{4}$ x 12 = $\frac{(1x12)}{4}$ = $\frac{12}{4}$ = 3
c). Bij het delen van een breuk door een heel getal, deel je de teller door dat getal.
1 $\frac{4}{8}$ : 2 = $\frac{12}{8}$ : 2 = $\frac{(12:2)}{8}$ = $\frac{6}{8}$.
Het toepassingsprobleem van het vermenigvuldigen van een breuk met een heel getal krijgt in de volgende les de uitleg:
In groep 7A zitten 25 kinderen.
$\frac{2}{5}$ deel van de kinderen in groep 7A doet niet aan sport.
Hoeveel kinderen zijn dat?
Stap 1. Maak een tekening van de vraag.
Stap 2. Wat moet je uitrekenen? $\frac{2}{5}$ x 25 = …
Stap 3. Wat is je antwoord? $\frac{2}{5}$ x 25 = $\frac{(2x25)}{5}$ = $\frac{50}{5}$ = 10.
Stap 4. Klopt je antwoord? Laat zien met een berekening.
1 groepje is $\frac{1}{5}$ deel van 25 = 5 kinderen.
2 groepjes is $\frac{1}{5}$ + $\frac{1}{5}$ = $\frac{2}{5}$ deel = 10 kinderen,
Het antwoord klopt.
De laatste stap 4 is de natuurlijke oplossing van het probleem.
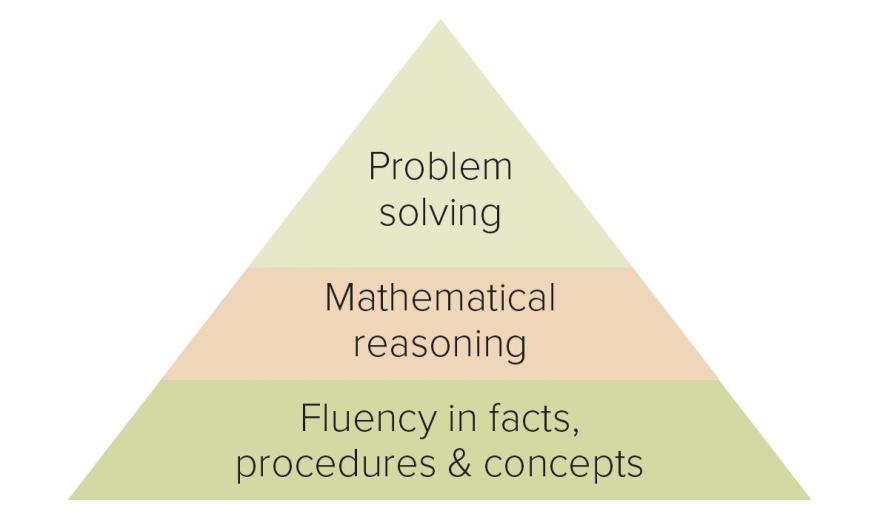
Anders gezegd: de onderste en de bovenste laag van de getoonde onderwijsdriehoek uit de inleiding staan hier anders om.
Dit voorbeeld laat meteen ook zien hoe ingrijpend het is om met een dichtgetimmerde EDI-methode naar een meer op IPO gerichte aanpak over te stappen (Muller, 2023; Liljedahl, 2021)
[i] Zie de videoles Master MT-304. https://www.youtube.com/watch?v=JIjUEm9HdPw
[ii] Basisfunctie (2) van toegepast probleemoplossen laten we in de basistekst onbesproken. Een voorbeeld daarvan:
$\frac{1}{a}$ + $\frac{1}{b}$ + $\frac{1}{c}$ = 1
De letters a , b en c verwijzen naar verschillende getallen.
Bepaal die drie getallen op de plaatsen van a, b en c. Lastiger is om te bewijzen dat er maar één getallendrietal voldoet. Opvallend is dat geschoolde rekenaars vaak meer moeite hebben om deze vragen te beantwoorden dan leerlingen uit de bovenbouw van de basisschool. En dat voert ons weer terug naar de eerder getoonde onderwijsdriehoek van Kirschner.
Kirschner et al. (2018) indicate that discovery learning and problem solving demand too much from students’ working memory. However, discovery learning and problem solving are central to the didactic approach used in the highest scoring countries. An analysis of fraction addition shows that approaches based on problem solving offer students more perspective than demonstrating and imitating, as for example is typical for the EDI approach.
Literatuur
[kop literatuur]Literatuur
De Jong, T., Lazonder, A. W., Chinn, C. C., Fischer, F., Gobert, J., Hmelo-Silver, C.E., Koedinger, K.R., Krajcik, J.S., Kyza, E.A., Linn, M.C., Pedaste, M., Scheiter, K., Zacharia, Z.C. (2023). Lets talk evidence - The case of combining inquiry-based and direct instruction. Educational Review, 39, 100536. https://www.sciencedirect.com/science/article/pii/S1747938X23000295
Getal & Ruimte (2017). Leerboek 7 A. Noordhoff.
Isoda, M. (2010). Elementary School Teaching Guide for Japanese Course of Study: Mathematics ( Grade 1-6). University of Tsukuba.
Kirschner, P. A., L. Claessens & S. Raaijmakers ( 2018). Op de schouders van reuzen. Ten Brink.
Kohn, A. (2024, 4 maart). Cognitive Load Theory: An Unpersuasive Attempt to Justify Direct Instruction. https://www.alfiekohn.org/blogs/clt/.
Liljedahl, P. (2021). Building Thinking Classrooms in Mathematics. 14 Teaching Practices for enhancing learning. Crown Press.
Mostert., T. & Hickendorff, M. (2024). Pizza of geen pizza? Helpt het geven van een context bij het rekenen van breuken? Volgens Bartjens, 43(3), 8-10.
Miao. Z. , Bokhove, C. & Reynolds, D. (2024). Master Mathematics Teachers Educational and Professional Excellence in Chinese Primary Schools. Routledge.
Muller, M. (2023) Gewoon meedoen in de klas. WiskundE-brief. https://www.wiskundebrief.nl/?901/-1
Takahashi, A. (2019). Characteristics of Japanese Mathematics Lessons. De Paul University.
Takahashi, A. (2021). Teaching Mathematics through Problem-solving. A Pedagogical Approach from Japan. Routledge.
